Üks kvantmehhaanika väiteid on see, et iga kvantosakest saab kirjeldada lainefunktsiooniga (sümboliga psii). Lainefunktsiooni järel tähistab x asukohta ja t aega. Lainefunktsiooni kaudu saab leida tõenäosuse, et osake asub x kohas t ajal. Kui x läheneb lõputusele, siis läheneb lainefunktsioon nullile. Üks psii tähistab tõenäosuse amplituuti ja psii ruudus annab tõenäosuse leida osakest mingist kohast.
Lainefunktsioon ei ole lihtne korrutustehe vaid selle kasutamisel peab leidma osatuletisi ning vahel läheb integraale vaja.
Tõenäosus leida osakest on 1 (100%), kui liita kokku osakese esinemise tõenäosused igas võimalikus punktis.
Lainefunktsioon on osaliselt imaginaararv (ülavalemites tähega j), mille ruut annab -1. Ülatärni (konjugaadi) esinemisel vahetatakse tehtes "+" ja "-" märgid. Lainefunktsiooni ja selle konjugaat korrutatakse omavahel ning selle käigus tekib imaginaararv ruudus, mis vahetatakse -1 vastu.
Kvantosakesi kirjeldav lainevõrrand sarnaneb osaliselt ühedimensioonilise nööril leviva laine võrrandiga:
Tasapinnalise elektromagnetkiirguse lainevõrrand.
Harmoonilise võnkumise võrrand ülal võrreldes selle kohal oleva võnkuva vedru potentsiaalse energia võrrandiga.
Lainefunktsiooni tuletis peab sisaldama konstanti ja x ruutu. Selline valem sobib lainefunktsioonina kuna kui x läheneks lõputusele, siis läheneks lainefunktsioon nullile.
Schrödingeri võrrandi lahendamisel saadav energia valem. Sellise harmoonilise võnkumise valemiga saab suhteliselt täpselt leida vibreerivate kahe aatomiga molekulide vibratsioonienergia asukoht kuigi täpsus langeb suuremate molekulidega.
Minimaalse energia leidmises alustades ülemise Schrödingeri valemiga.
Lihtsustatud kokkuvõttena antakse lainefunktsioonile ülemine kuju, mida kasutatakse tuletamises.
Pärast kahte tuletamist leitakse lainefunktsioon iga x väärtuse jaoks. X'i korrutav suurus a on püsiva väärtusega iga x väärtuse korral.
x ruutu panekud eemaldatakse mõlemast valemi poolest ja energia leidmiseks pandakse samade osakeste jaoks muutumatud suurused üksteisega võrdseks.
Saadud energia väärtus võrdub määramatuse printsiibi poolt minimaalse võimaliku energiaga, mis peaks esinema isegi jahutamisel absoluutse nullini. See energia võib olla põhjuseks, miks heelium atmosfäärirõhul ühegi temperatuuri juures ei külmu.
Võrdlus Newton'i võnkumise ja kvantmehhaanika vahel. Kvantmehhaanika kirjeldab hästi aatomi suurusjärgus osakesi ning Newton'i seadused suuri objekte. Vähemalt osades olukordades paistab nende kahe vahel peaaegu vastupidine käitumine.
Roosa alaga on tähistatud minimaalse energiaga lainefunktsioon psii null ruuduga ja hallide täppidega suure objekti käitumine. Mõlemas suurusjärgus toimuks võnkumine kahe punaselt tähistatud vertikaalse piiri vahel. Kõrgemal olek tähistab suuremat esinemise tõenäosust selles punktis. Vetruv suur objekt, mis kõiguks kahe seina vahel oleks kõige lühemat aega ruumi keskel kuna see lendaks kiiresti edasi ruumi teise otsa olles rohkem aega keskosast eemal. Kvantosakeste puhul paistab käitumine vastupidine. Võnkuv osake asub kauem ruumi keskel levides keskosast suhteliselt harva eemale. Ühe lisaomadusena on kvantosakesed barjääride poolt vähem piiratud ja võivad neid läbida (quantum tunneling).
Kui kvantosake on energilisem (suurema psii all näidatud kvantarvuga), siis käitub see suure objektiga sarnasemalt.
Kui kvantarv n=10, siis on kvantosakese asukoht ruumis sarnasem igapäevaelus paistva võnkuva objektiga olles kauem võnkumise piirialadel. Lainefunktsiooniga jääb kaduv ja taastekkiv esinemise tõenäosus, mis teeb tõenäosusjaotuse lünklikuks. Suurema n väärtusega lähenevad nende tõenäosuste tipud üksteisele.
Piisavalt suure n väärtusega ei oleks need tipud täpselt eristatavad, sest määramatuse printsiip piirab täpseid teadmisi kvantosakeste asukohast mingis ajas.
Klassikalise füüsika järgi ei saa osake läbida barjääri (quantum tunneling), kui osakese energia on vähem kui läbimiseks vajalik energia U0. Kvantfüüsikas võivad osakesed takistusi läbida kaotamata energiat kuigi väheneb tõenäosus, et osake esineb teisel pool takistust. Lainefunktsioon ise peab olema jätkuv isegi kui pool lainet jääks seina sisse või teisele poole takistust. Samas langeb seina läbiva osakese esinemise tõenäosus eksponentsiaalselt piirkonnas, kus lainefunktsioon läbib seina.
Lainefunktsiooni valem kui see läbib takistust energiabarjääriga U0. Alfa on nõrgenemise faktor ning mida suurem see on, seda rohkem lainefunktsiooni suurus väheneb. Mida suurem on osakese mass või mida suurem on U0 osakese energiaga võrreldes seda väiksema tõenäosusega läbib see takistust.














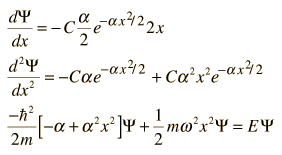






No comments:
Post a Comment